誤差(error)とは、観測された値と真の値との差。(しかし、真の値は基本的にはわからない)
残差(residual)とは、観測された値と予測値との差。(予測値は、回帰モデルなどで推定を行うことで分かる)
統計的手法の前提として、正規性や独立性などが挙げられるとき、本来であればそれは誤差に対して適用される。しかし、実際には誤差はわからないので、代わりに残差を用いて判断することになる。
Rで残差を確認する方法
Rで残差を確認する関数には、resid() がある。()内には、回帰モデルのオブジェクトを入れる。
resid(model1)回帰分析と誤差の関係
単回帰式:Y=α+βX+ε
Y=切片+傾き+誤差
重回帰式: Y=α+β₁X₁+β₂X₂+…+βnXn+ε
Y=切片+傾き1+傾き2…+傾きn+誤差
回帰分析(単回帰や重回帰)では、最小二乗法を用いることによって回帰直線を決定する。回帰直線において、切片(y)は独立変数が0のときの従属変数の値を示し、反対に、切片(X)は従属変数が0のときの独立変数を値を示す。また、独立変数が1増加したときの従属変数の増加量は回帰係数(β)で示される。誤差は、これらでは説明のできないばらつきである。回帰分析において、誤差は正規分布していること(Normality)、期待値は0であること、それぞれが独立していること(Independence)、分散は均一であること(Homoscedasticity)などを仮定としている。
診断プロット
これらの残差に関する仮定を簡単に確認する方法として、診断プロットがある。
診断プロットは、plot()の()内にモデルのオブジェクト名を入力すると確認できる。
par(mfrow=c(2,2)) #2×2で一覧表示させる
plot(model1) #診断プロットを作成回帰診断プロットでは、以下のようにグラフが表示される。
- Residuals vs Fitted :非線形性、分散不均一、外れ値を確認できる。
- NormalQ-Q(正規Q-Qプロット)
- Scale-Location
- Residuals vs Leverage(+Cook’s distance)、Constant Leverage: Residuals vs Factor level… ※モデルによって異なる
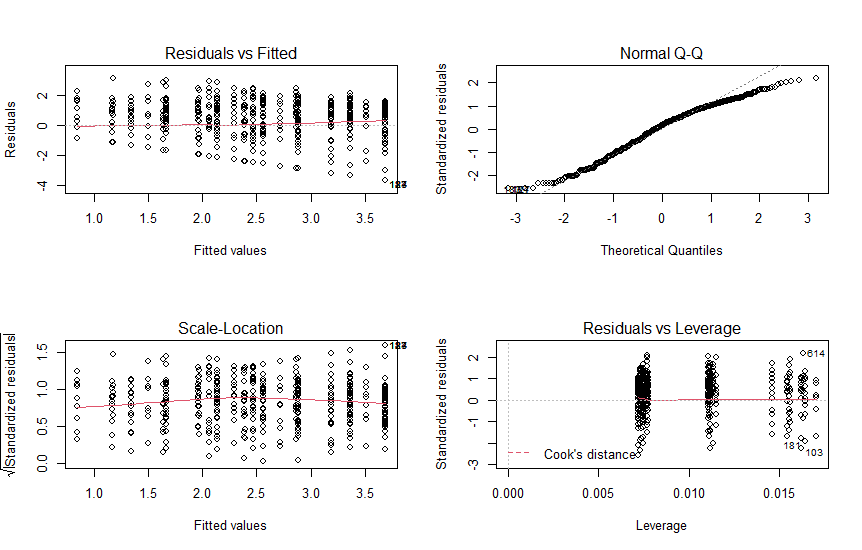
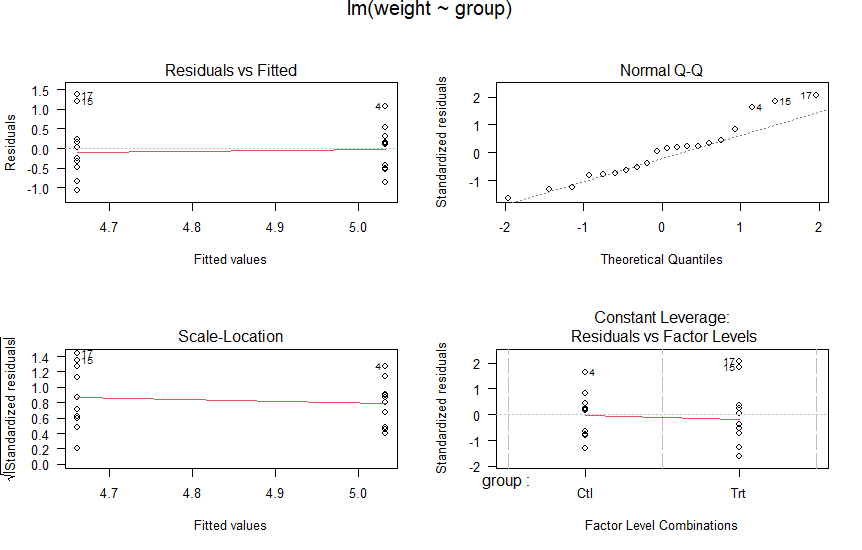
From: lm function – RDocumentation サンプルコード
診断プロットの見方
線 形 性:残差が0の線の周りにばらけて分布している
分散の均一性:残差が0の線の周りに水平な帯状に並んでいる
外れ値の有無:残差の分布パターンから明らかに外れている点がないか
残差が正規分布しているかを確認することができる。縦軸は正規分布を仮定した場合の期待値、横軸は正規分布の分位数。
残差が正規分布に従っている場合は、一直線状にプロットされる。
ちなみに、Q-Qの「Q」は、quantileの頭文字
※これらは、あくまで主観的な確認方法であることに注意する。
メモ
- 分散不均一性を調べる方法として、残差の平方を被説明変数として回帰分析を行い、全ての説明変数の係数が0であるかを検定する方法がある。
参考
- STAT 462. 4.2 – Residuals vs. Fits Plot. https://online.stat.psu.edu/stat462/node/117/. 2021/8/1アクセス.
- 重回帰分析.https://www.statistics.co.jp/reference/software_R/statR_6_reg2.pdf, 2021/8/1アクセス.
- 回帰分析 重回帰(3).http://fs1.law.keio.ac.jp/~aso/ecnm/pp/ecnmtrcs06.pdf. 2021/8/1アクセス.
